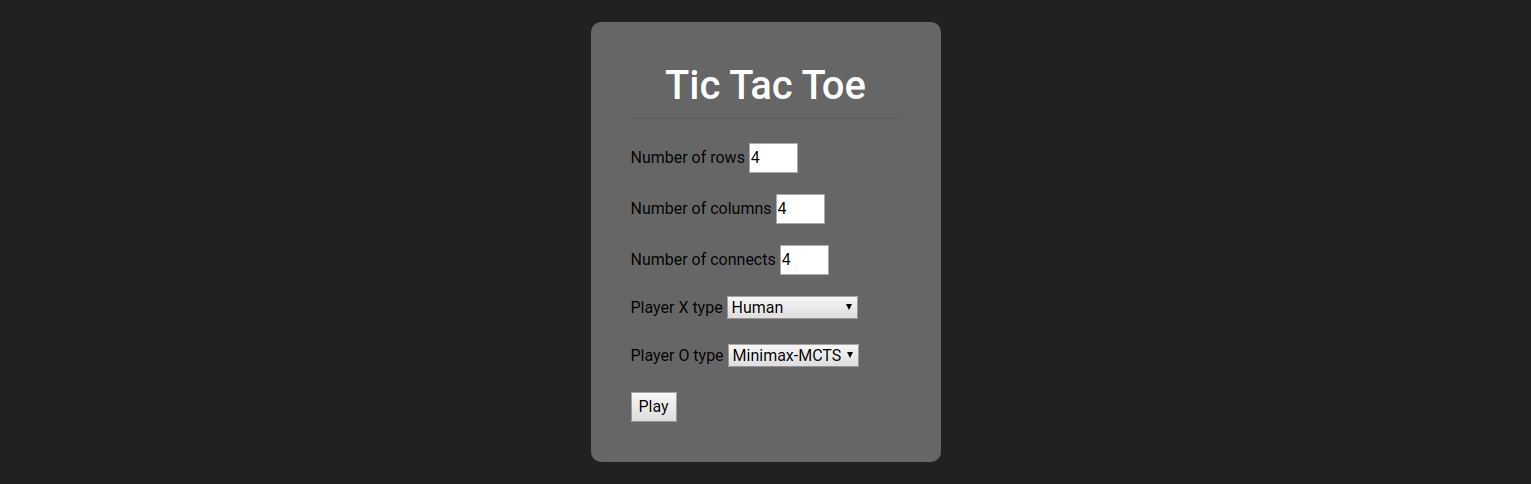
Generalized Tic Tac Toe web app

TL;DRPermalink

A project to investigate tree search based AI on the generalized classic game of Tic Tac Toe where both the dimensions and the number of connects to win are configurable. Implemented AI algorithms include iterative-deepening minimax and Monte Carlo Tree Search (MCTS). The app is available at https://tictactoe-minimax.herokuapp.com/. Note that it can take a while to load at first since I am using the free dyno of Heroku.

How I came about this idea?Permalink

I was interested in AI algorithms and thought it would be fun to do quick project on the classic Tic Tac Toe game. Of course, the classic 3x3x3 game is a bit too simplistic to require any involved algorithms. Therefore, I decided to generalize the game as a $n\times m\times c$, where $n\times m$ is the dimensions of the game and $c$ is the number of connects one need to win, e.g., the classic game is 3. Also, I thought it would be interesting to be able to pitch different AI algorithms against each other so one can simply spectate their match.

Tech stackPermalink

• Django: used to build the web app.
• Postgres: used to manage the game info.

Technical challengesPermalink

While it is easy to traverse the whole game tree for a $3\times 3$ game, approximations is certainly need for a $5\times 5$ game (at least if the implementation is in Python) where the second move has a state-space of 24!. Also, it was desirable to keep the memory footprint of each state node small. As such, some of the challenges include:

• Small state nodes: by restricting the max board dimension as a $5\times 5$ board, each state can be represented as a $2^{25}$-bit board which fits into a Python $2^{31}$ int. Yeah… it’s pretty satisfying to have the need to play at the bit level.
• Different approximation techniques including heuristics function of incomplete board state, transposition board, and more involved algorithms, e.g., iterative deepening and MCTS, are used.

The code is available at Github.